Normal Prior, several observations

# sphinx_gallery_thumbnail_number = -1

import arviz as az
import matplotlib.pyplot as plt
import pyro
import pyro.distributions as dist
import torch
from matplotlib.ticker import StrMethodFormatter

from gempy_probability.plot_posterior import PlotPosterior
from pyro.infer import Predictive, NUTS, MCMC

y_obs = torch.tensor([2.12])
y_obs_list = torch.tensor([2.12, 2.06, 2.08, 2.05, 2.08, 2.09,
                           2.19, 2.07, 2.16, 2.11, 2.13, 1.92])
pyro.set_rng_seed(4003)

Setting Backend To: AvailableBackends.numpy

def model(distributions_family, data):
    if distributions_family == "normal_distribution":
        mu = pyro.sample('$\mu$', dist.Normal(2.07, 0.07))
    elif distributions_family in "uniform_distribution":
        mu = pyro.sample('$\mu$', dist.Uniform(0, 10))
    else:
        raise ValueError("distributions_family must be either 'normal_distribution' or 'uniform_distribution'")
    sigma = pyro.sample('$\sigma$', dist.Gamma(0.3, 3))
    y = pyro.sample('$y$', dist.Normal(mu, sigma), obs=data)
    return y

1. Prior Sampling

prior = Predictive(model, num_samples=100)("normal_distribution", y_obs_list)
# 2. MCMC Sampling
nuts_kernel = NUTS(model)
mcmc = MCMC(nuts_kernel, num_samples=1000, warmup_steps=100)  # Assuming 1000 warmup steps
mcmc.run("normal_distribution", y_obs_list)
# Get posterior samples
posterior_samples = mcmc.get_samples(1100)
# 3. Sample from Posterior Predictive
posterior_predictive = Predictive(model, posterior_samples)("normal_distribution", y_obs_list)

Warmup:   0%|                                                       | 0/1100 [00:00, ?it/s]
Warmup:   2%|▎           | 26/1100 [00:00, 243.34it/s, step size=2.54e-02, acc. prob=0.747]
Warmup:   5%|▌           | 51/1100 [00:00, 148.51it/s, step size=1.99e-02, acc. prob=0.765]
Warmup:   7%|▊           | 73/1100 [00:00, 166.60it/s, step size=2.68e-02, acc. prob=0.774]
Warmup:   9%|█           | 97/1100 [00:00, 180.82it/s, step size=1.57e-01, acc. prob=0.772]
Sample:  11%|█▏         | 121/1100 [00:00, 198.02it/s, step size=2.71e-01, acc. prob=0.946]
Sample:  13%|█▍         | 148/1100 [00:00, 218.96it/s, step size=2.71e-01, acc. prob=0.955]
Sample:  16%|█▋         | 172/1100 [00:00, 223.29it/s, step size=2.71e-01, acc. prob=0.952]
Sample:  18%|█▉         | 198/1100 [00:00, 233.24it/s, step size=2.71e-01, acc. prob=0.955]
Sample:  21%|██▎        | 229/1100 [00:01, 255.61it/s, step size=2.71e-01, acc. prob=0.949]
Sample:  23%|██▌        | 258/1100 [00:01, 263.11it/s, step size=2.71e-01, acc. prob=0.949]
Sample:  26%|██▊        | 285/1100 [00:01, 263.56it/s, step size=2.71e-01, acc. prob=0.951]
Sample:  29%|███▏       | 314/1100 [00:01, 269.45it/s, step size=2.71e-01, acc. prob=0.951]
Sample:  31%|███▍       | 342/1100 [00:01, 272.39it/s, step size=2.71e-01, acc. prob=0.951]
Sample:  34%|███▋       | 373/1100 [00:01, 281.13it/s, step size=2.71e-01, acc. prob=0.947]
Sample:  37%|████       | 402/1100 [00:01, 268.66it/s, step size=2.71e-01, acc. prob=0.946]
Sample:  39%|████▎      | 430/1100 [00:01, 266.02it/s, step size=2.71e-01, acc. prob=0.944]
Sample:  42%|████▌      | 461/1100 [00:01, 276.21it/s, step size=2.71e-01, acc. prob=0.941]
Sample:  45%|████▉      | 498/1100 [00:01, 301.13it/s, step size=2.71e-01, acc. prob=0.939]
Sample:  48%|█████▎     | 529/1100 [00:02, 292.94it/s, step size=2.71e-01, acc. prob=0.938]
Sample:  51%|█████▌     | 559/1100 [00:02, 292.06it/s, step size=2.71e-01, acc. prob=0.940]
Sample:  54%|█████▉     | 589/1100 [00:02, 284.27it/s, step size=2.71e-01, acc. prob=0.941]
Sample:  56%|██████▏    | 618/1100 [00:02, 268.08it/s, step size=2.71e-01, acc. prob=0.941]
Sample:  59%|██████▍    | 646/1100 [00:02, 244.63it/s, step size=2.71e-01, acc. prob=0.941]
Sample:  62%|██████▊    | 679/1100 [00:02, 266.39it/s, step size=2.71e-01, acc. prob=0.941]
Sample:  65%|███████    | 710/1100 [00:02, 275.78it/s, step size=2.71e-01, acc. prob=0.942]
Sample:  67%|███████▍   | 739/1100 [00:02, 276.86it/s, step size=2.71e-01, acc. prob=0.942]
Sample:  70%|███████▋   | 768/1100 [00:03, 263.63it/s, step size=2.71e-01, acc. prob=0.942]
Sample:  72%|███████▉   | 795/1100 [00:03, 255.34it/s, step size=2.71e-01, acc. prob=0.942]
Sample:  75%|████████▎  | 825/1100 [00:03, 266.68it/s, step size=2.71e-01, acc. prob=0.942]
Sample:  77%|████████▌  | 852/1100 [00:03, 258.75it/s, step size=2.71e-01, acc. prob=0.941]
Sample:  80%|████████▊  | 881/1100 [00:03, 266.17it/s, step size=2.71e-01, acc. prob=0.942]
Sample:  83%|█████████  | 910/1100 [00:03, 269.62it/s, step size=2.71e-01, acc. prob=0.942]
Sample:  85%|█████████▍ | 938/1100 [00:03, 266.48it/s, step size=2.71e-01, acc. prob=0.942]
Sample:  88%|█████████▋ | 965/1100 [00:03, 263.00it/s, step size=2.71e-01, acc. prob=0.942]
Sample:  90%|█████████▉ | 992/1100 [00:03, 260.45it/s, step size=2.71e-01, acc. prob=0.942]
Sample:  93%|█████████▎| 1019/1100 [00:03, 258.64it/s, step size=2.71e-01, acc. prob=0.942]
Sample:  95%|█████████▌| 1045/1100 [00:04, 255.68it/s, step size=2.71e-01, acc. prob=0.942]
Sample:  97%|█████████▋| 1071/1100 [00:04, 249.31it/s, step size=2.71e-01, acc. prob=0.943]
Sample: 100%|█████████▉| 1099/1100 [00:04, 255.38it/s, step size=2.71e-01, acc. prob=0.943]
Sample: 100%|██████████| 1100/1100 [00:04, 255.61it/s, step size=2.71e-01, acc. prob=0.943]

data = az.from_pyro(
    posterior=mcmc,
    prior=prior,
    posterior_predictive=posterior_predictive
)
az_data = data
az.plot_trace(az_data)
plt.show()

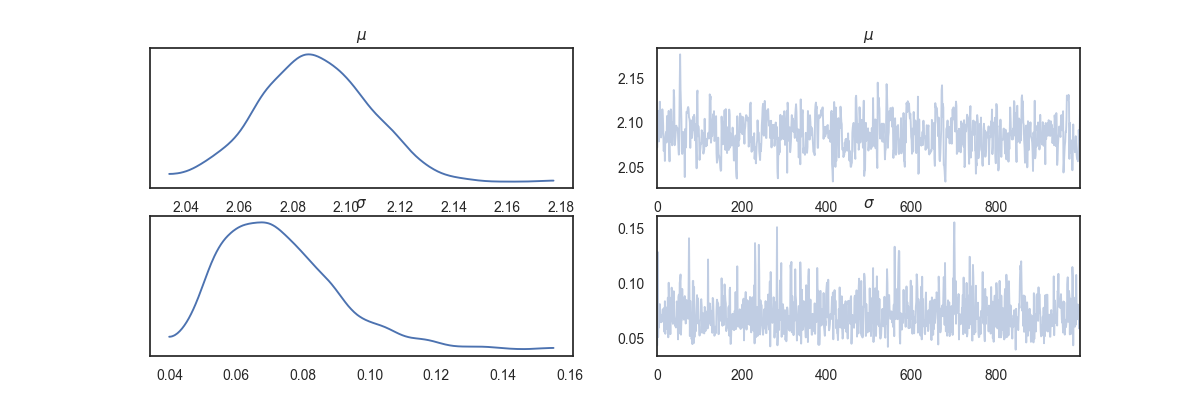
C:\Users\MigueldelaVarga\PycharmProjects\VisualBayesic\venv\lib\site-packages\arviz\data\io_pyro.py:157: UserWarning: Could not get vectorized trace, log_likelihood group will be omitted. Check your model vectorization or set log_likelihood=False
  warnings.warn(
posterior predictive shape not compatible with number of chains and draws.This can mean that some draws or even whole chains are not represented.

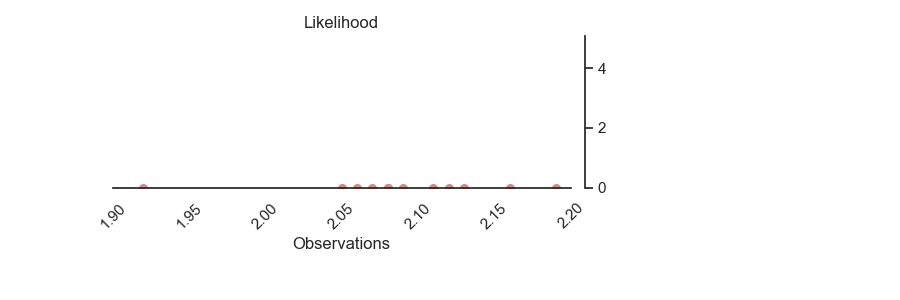
p = PlotPosterior(az_data)
p.create_figure(figsize=(9, 3), joyplot=False, marginal=False)
p.plot_normal_likelihood('$\mu$', '$\sigma$', '$y$', iteration=-1, hide_bell=True)
p.likelihood_axes.set_xlim(1.90, 2.2)
p.likelihood_axes.xaxis.set_major_formatter(StrMethodFormatter('{x:,.2f}'))
for tick in p.likelihood_axes.get_xticklabels():
    tick.set_rotation(45)
plt.show()

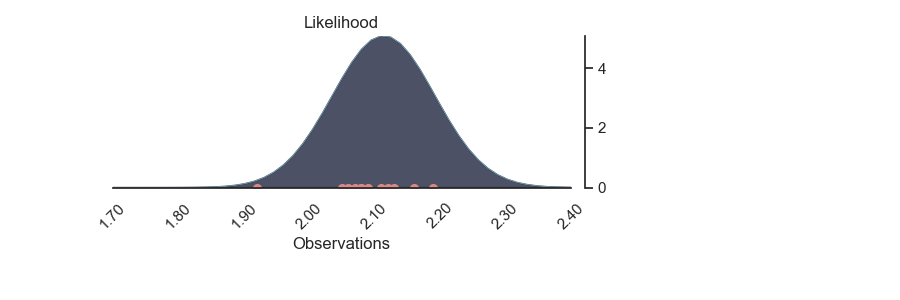
p = PlotPosterior(az_data)
p.create_figure(figsize=(9, 3), joyplot=False, marginal=False)
p.plot_normal_likelihood('$\mu$', '$\sigma$', '$y$', iteration=-1, hide_lines=True)
p.likelihood_axes.set_xlim(1.70, 2.40)
p.likelihood_axes.xaxis.set_major_formatter(StrMethodFormatter('{x:,.2f}'))
for tick in p.likelihood_axes.get_xticklabels():
    tick.set_rotation(45)
plt.show()

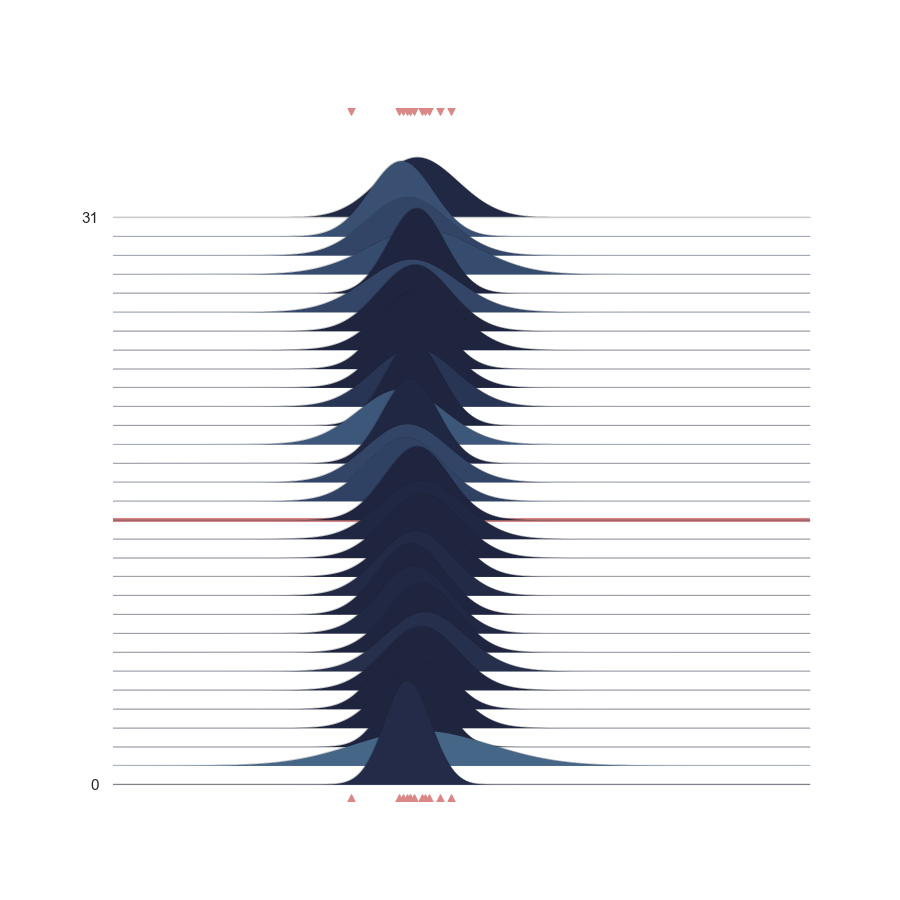
p = PlotPosterior(az_data)

p.create_figure(figsize=(9, 9), joyplot=True, marginal=False, likelihood=False, n_samples=31)
p.plot_joy(('$\mu$', '$\sigma$'), '$y$', iteration=14)
plt.show()

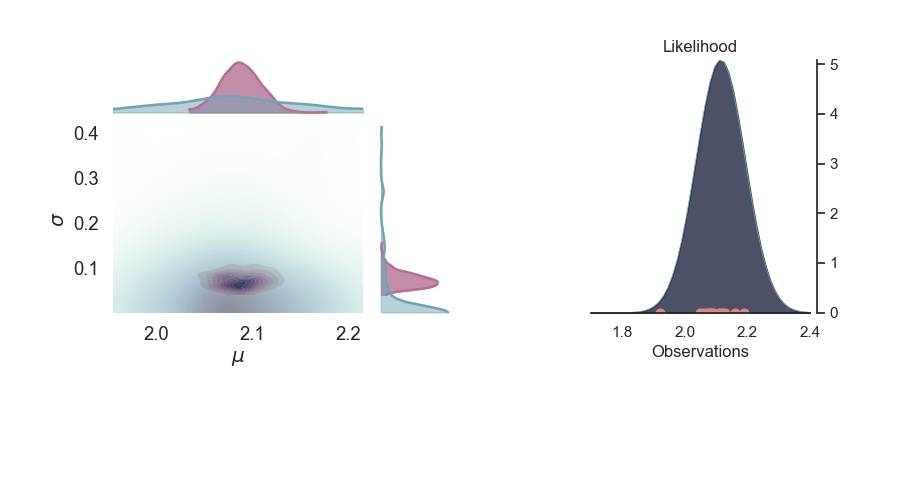
p = PlotPosterior(az_data)

p.create_figure(figsize=(9, 5), joyplot=False, marginal=True, likelihood=True)
p.plot_marginal(
    var_names=['$\mu$', '$\sigma$'],
    plot_trace=False,
    credible_interval=0.95,
    kind='kde',
    joint_kwargs={'contour': True, 'pcolormesh_kwargs': {}},
    joint_kwargs_prior={'contour': False, 'pcolormesh_kwargs': {}})

p.plot_normal_likelihood('$\mu$', '$\sigma$', '$y$', iteration=-1, hide_lines=True)
p.likelihood_axes.set_xlim(1.70, 2.40)

plt.show()

License

The code in this case study is copyrighted by Miguel de la Varga and licensed under the new BSD (3-clause) license:

https://opensource.org/licenses/BSD-3-Clause

The text and figures in this case study are copyrighted by Miguel de la Varga and licensed under the CC BY-NC 4.0 license:

https://creativecommons.org/licenses/by-nc/4.0/ Make sure to replace the links with actual hyperlinks if you’re using a platform that supports it (e.g., Markdown or HTML). Otherwise, the plain URLs work fine for plain text.